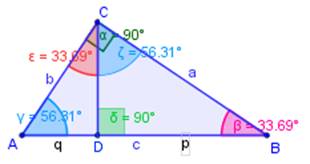
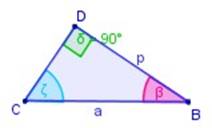
La trigonometría esférica es la aplicación de los métodos de la trigonometría al estudio de ángulos, lados y áreas de triángulos esféricos y otros polígonos. Un triángulo esférico es un triángulo construido sobre una esfera, con tres vértices y tres lados que son arcos de círculo máximo. Los ángulos de un triángulo esférico no suman 180 grados. De hecho, la suma puede hallarse entre 180 y 540 grados. Considérese, por ejemplo, un triángulo esférico con un vértice en el Polo Norte y los otros dos vértices en el ecuador de la Tierra. La resolución de triángulos esféricos adquiere particular importancia en astronomía y navegación para determinar la posición de un buque en mar abierto mediante la observación de los astros.
A lo largo de los siglos, con sus funciones fundamentales (seno, coseno, tangente, cotangente, secante y cosecante), la disciplina constituyó el nervio de la educación matemática. Fue materia troncal en las escuelas superiores hasta los años cincuenta de la postrera centuria. Hoy apenas si se enseña. Se trata de una especie en extinción, cuya rica historia y persistente apogeo traza Heavenly mathematics. La Grecia clásica, el Islam medieval y el Occidente moderno utilizaron la trigonometría esférica para cartografiar el firmamento y la Tierra, como demuestra y actualiza Glen van Brummelen, coordinador de matemática y de ciencias físicas en la Universidad Quest, presidente de la Sociedad Canadiense de Historia y Filosofía de la Ciencia y autor, entre otros textos afines, de The mathematics of the heavens and the earth: The early history of trigonometry y Mathematics and the historian's craft.
Los contenidos de los manuales de matemáticas han cambiado drásticamente. En la mente de todos está la revolución traída por el colectivo Nicolas Bourbaki. Sin llegar a esa radicalidad, y abrimos un tratado de hace un siglo, reconoceremos temas que nos serán familiares, pero otros nos resultarán desconocidos o, cuando menos, desconcertantes. Un texto avanzado de geometría analítica, por ejemplo, contenía involutas de círculos, hipocicloides y círculos auxiliares de las elipses, cuestiones del todo ajenas al alumno de nuestros días. Pero será la trigonometría esférica el ejemplo mas espectacular de cambios en el aula de matemática del siglo XX. Todavía en el primer tercio, las ediciones de losElementos de Euclides ideadas para el aula contenían apéndices obligados sobre trigonometría. Durante la Segunda Guerra Mundial, la popularidad de la trigonometría esférica persistió. Ocupaba un puesto destacado en la enseñanza y en la praxis naval y militar. Mas, poco a poco, fue relegándose hasta desaparecer de unos textos centrados ya de manera exclusiva en la trigonometría plana. Una pérdida que resulta particularmente sorprendente en unos momentos en que se están descubriendo nuevas aplicaciones. Algunas de las fórmulas del GPS se han construido sobre la misma. Ahora, muy pocos manuales, por ejemplo, se preguntan por qué sen(α + β) = senα ⋅ cosβ + cosα ⋅ senβ. Pero eso es culpa de los manuales, no del tema.
Parece obvio que no podamos determinar las dimensiones de la Tierra midiéndola directamente y haya que recurrir a aproximaciones indirectas. La historia recoge uno de los primeros y más ingeniosos métodos, el de Eratóstenes de Cirene, astrónomo griego del siglo III antes de Cristo; se servía de la observación de la penetración de la luz solar en pozos de distintas localidades. Hiparco de Rodas, del siglo II a.C., natural de Bitinia, conocía los movimientos del firmamento. También los astrónomos babilonios que le precedieron. Pero Hiparco abrió un nuevo surco cuando examinó el movimiento del Sol. Hoy sabemos que el Sol viaja a lo largo de la eclíptica. Para averiguar cuánto se movía el astro de su centro, Hiparco inventó la función de la cuerda (que más tarde, en la India, se cambió en función seno) y, por tanto, fundó la ciencia de la trigonometría. Una vez convirtió Hiparco la longitud del día estacional en grados, todo lo que necesitaba para hallar la distancia de la Tierra al centro eran un par de longitudes de cuerda y geometría elemental. Fue la determinación de esa cantidad, la excentricidad de la órbita solar, lo que pudo haber sido el primer problema trigonométrico del mundo.
Una cosa es calcular el tamaño de la Tierra y otro aventurarse más allá de los límites de la Tierra y medir distancias, por ejemplo, de la Luna. Lo intentó Claudio Ptolomeo, científico alejandrino del siglo II d.C., quien llegó a un valor bastante aproximado. Ptolomeo calculó también la distancia al Sol, con mucha menor precisión. La clave está en la paralaje: el hecho de que dos observadores, situados en diferentes lugares, verán el mismo objeto en diferente posición con respecto al fondo distante. A Ptolomeo debemos también las primeras tablas trigonométricas. Su monumental Colección matemáticacontiene un conjunto notable de modelos sobre los movimientos de los cuerpos celestes. Situó la Tierra en el centro del universo (geocentrismo), una teoría que condicionó la astronomía a lo largo de un milenio y medio. Se tradujo al árabe con el título Kitab al-majisti, el Almagesto. El primero de esos libros contiene una descripción de cómo se puede construir una tabla trigonométrica con pluma y papel. (Ptolomeo empleó otra función, la cuerda.)
La revolución en la trigonometría geométrica llegó con la ilustración islámica en torno al primer milenio. Abu Sahl al-Kuhi vivió en Bagdad durante las últimas décadas del siglo X. Interesado en la astronomía, su estilo recordaba el de Euclides, Arquímedes y Apolonio. Considerado hoy el geómetra más importante del siglo X, también se le recuerda por un error desafortunado; al fiar demasiado en una analogía geométrica que había descubierto entre ciertas formas en su obra sobre centros de gravedad extrajo la conclusión de que π = 3 1/9. Abu Nasr Mansur ibn Ali ibn Iraq descubrió el triángulo polar. En el Libro del azimuth Abu Nasr propuso la regla de las cuatro cantidades, el primer ejemplo del principio de localidad. Imaginémonos un triángulo esférico cuyo tamaño se va encogiendo hasta que está a punto de desaparecer. A medida que va empequeñeciéndose comienza a parecerse a un triángulo plano. Por consiguiente, cualquier enunciado sobre un triángulo esférico, aplicado a un triángulo que se va encogiendo hasta casi desaparecer, se convierte en un enunciado sobre un triángulo plano. La regla de las cuatro cantidades está relacionada con un teorema mucho más conocido hoy, la ley esférica de los senos.
Discípulo de Nasr Mansur fue Abu al-Rayhan Muhammad ibn Ahmad al-Biruni (973-1050), quien escribió tratados sobre todas las ciencias conocidas de su tiempo: mecánica, medicina y mineralogía, además de matemáticas y astronomía. Su Kitab Tahdid al-Amakin (Libro sobre la determinación de las coordenadas de las ciudades) se inspiró originalmente en el problema de hallar la qibla, la referencia a La Meca, en cuya dirección los musulmanes deben rezar. El libro es una descripción exhaustiva de técnicas matemáticas para localizar ciudades en la superficie de la Tierra; utiliza métodos trigonométricos (regla de las cuatro cantidades y ley del seno). Fue, en efecto, una preocupación religiosa lo que hizo que los trigonómetras volvieran los ojos a la Tierra. La práctica del Islam obliga al fiel a cumplir cinco compromisos, llamados los Cinco Pilares. La astronomía no sirve de particular ayuda en tres de ellos (profesión de fe, obras de caridad y la hajj, o peregrinación a La Meca); pero en los dos restantes —ayuno durante las horas de luz solar en el mes del Ramadán y las cinco plegarias diarias— sí requerían asistencia técnica. Sea el ayuno mensual. El calendario árabe es lunar, de forma que cada mes comienza cuando reaparece el cuarto creciente detrás del Sol. Si perdemos el creciente de un día particular, podríamos terminar violando las exigencias del ayuno. Las cinco plegarias están reguladas por la posición del Sol en el firmamento. Deben dirigir su mirada hacia la Kaaba, una construcción cúbica que aloja la Piedra Negra; es el destino de la peregrinación que los musulmanes deben realizar una vez en su vida. La dirección de la Kaaba —la qibla— cumple otras funciones además de la plegaria diaria. Incluye determinar la dirección en la que los difuntos musulmanes deben quedar expuestos. Para calcular la qibla deben conocerse la posición de La Meca y la del orante. Nació así una floreciente industria de creación de tablas de la qibla para cualquier localidad. Las mejores fueron las calculadas por Shama al-Din al-Khalili, astrónomo oficial de la mezquita omeya de Damasco.
Mucho antes de que se inventaran los logaritmos o se crearan reglas de cálculo, los cálculos se hacían a mano. Pero incluso en la antigüedad hubo herramientas que facilitaban la tarea. Por ejemplo, la esfera armilar. Se trata de un modelo de esfera celeste que gira en el mismo sentido en que lo hace el firmamento. Para el manejo de la esfera armilar, necesitamos una proyección de la esfera celeste en una superficie plana. Se intentaron varias proyecciones de la esfera. La más común fue la proyección estereográfica. En ella, los círculos de la esfera se transforman en círculos sobre un plano; y conserva los ángulos. Las proyecciones han constituido el corazón de la geometría y de la trigonometría durante siglos.
El conjunto más prodigioso de tablas trigonométricas a lo largo del siglo XVI, el Opus palatinum, fue compuesto por Georg Rheticus, uno de los primeros defensores del heliocentrismo de Copérnico; su método no difiere sustancialmente del empleado por Ptolomeo. Rheticus murió en 1574, antes de terminar su obra, aunque sí estaban acabadas las tablas, que fueron publicadas en 1596 por Lucius Valentín Otho. Hay tablas de todas las funciones trigonométricas; en su forma modificada, persistieron hasta que fueron sustituidas en 1915.
Hubo otros intentos. Ciento cincuenta años antes de Rheticus, el astrónomo persa Jamshid al-Kashi había considerado el problema del seno 1o de una forma propia. Este maestro del cómputo, calculó el valor de π hasta el equivalente a 14 decimales.
Tardía fue, sin embargo, la introducción de la palabra «trigonometría», etimológicamente «medición de los triángulos». Empezó a emplearla Bartholomaeus Pitiscus, quien en 1600 publicó Trigonometriae, sive de dimensione triangulorum libri quinque. Hasta entonces se empleaba la expresión «ciencia de los triángulos». Más allá del término, en el siglo XVII John Napier (1550-1617) le dio un gran impulso con la invención de un procedimiento de extraordinario alcance; el descubrimiento de que los productos de potencias de diez los convertía en suma de exponentes (103 × 104 = 107) constituye el punto de arranque que le condujo a los logaritmos, descritos en su Mirifici logarithmorum canonis descriptio(1614). Tras un capítulo introductorio sobre definiciones básicas, el resto de la obra está dedicado a la ciencia de los triángulos en su variedad esférica. Para Pierre Simeon de Laplace el trabajo sobre los logaritmos, al abreviar la tarea, dobló la vida del astrónomo.